5/5 – (3 bình chọn)
FEM là gì? Fem hay còn được gọi là mô hình tác động cố định (Fixed Effects Model) là một trong các dạng phổ biến của mô hình dữ liệu bảng (Panel data model) bên cạnh mô hình tác động ngẫu nhiên REM (Random Effects Model). Mô hình FEM – hồi tác động cố định (Fixed-effects) và REM – tác động ngẫu nhiên (random-effects) được sử dụng trong phân tích dữ liệu bảng (hay còn gọi là dữ liệu dài: longitudinal data).
Bài viết dưới MOSL xin giới thiệu toàn bộ khái niệm và các kiểm định xoay quanh các mô hình Pooled OLS là gì?, FEM là gì?, REM là gì?, GLS và FGLS là gì? gồm Hausman Test, Breusch – Pagan LM test, F Test, Chow Test,…
1. Dữ liệu bảng Paneldata là gì?
Dữ liệu bảng là tập hợp của hai loại dữ liệu chuỗi thời gian (time – series) và dữ liệu chéo (Cross-setional).
Tham khảo thêm bài viết chuyên sâu về Dữ liệu bảng – panel data là gì? của MOSL nhé!
Mô hình hồi quy dữ liệu bảng điều khiển chung có dạng: 
Trong đó:
là biến phụ thuộc
là biến độc lập
vàlà các hệ số,
vàlà các chỉ số cho cá nhân và thời gian.
là rất quan trọng trong phân tích này.
Các giả định về thuật ngữ lỗi xác định khi nói về các tác động cố định (FE) hay tác động ngẫu nhiên (RE).
- Trong một mô hình hiệu ứng cố định (FEM),
- Trong một mô hình hiệu ứng ngẫu nhiên (REM),
Khái niệm về hai mô hình REM và FEM là gì? sẽ được Mosl trình bày chi tiết trong các phần phía dưới các bạn hãy kéo xuống xem nhé!
Phân tích dữ liệu bảng có ba cách tiếp cận độc lập:
- Các mô hình Pooled OLS tổng hợp độc lập;
- Các mô hình hiệu ứng ngẫu nhiên (REM) ;
- Mô hình hiệu ứng cố định (FEM) hoặc mô hình khác biệt đầu tiên.
Chú ý: Việc lựa chọn giữa các phương pháp này phụ thuộc vào mục tiêu của phân tích và các vấn đề liên quan đến tính đồng nhất của các biến giải thích.
Xem ngay: Mô hình phương pháp bình phương tối thiểu – OLS hay Pooled OLS là gì?
2. Mô hình tác động cố định (Fixed Effect Model) – FEM là gì?
Xét một mối quan hệ kinh tế với biến phụ thuộc Y và 2 biến độc lập là X1 và X2. Chúng ta có dữ liệu bảng cho Y, X1, và X2, gồm N-đối tượng và T-thời điểm, và vì vậy chúng ta có NxT quan sát.
Mô hình hồi quy tuyến tính cổ điển không có hệ số cắt được xác định bởi:
Yit = β1Xit + β2Xit + μitit với i = 1, 2, …, N và t = 1, 2, …, T (Mô hình *)
Phương trình trên được gọi là mô hình hồi quy các ảnh hưởng cố định (FEM – fixed effects regression model). Thuật ngữ “các ảnh hưởng cố định” là vì sự thật rằng mỗi hệ số cắt của biến độc lập, mặc dù khác nhau giữa các hệ số cắt của N-Đối tượng khác nhau, nhưng không thay đổi qua thời gian (time – invariant).
Hiệu ứng cố định (FE) là một kỹ thuật bình phương nhỏ nhất tổng quát khả thi (FGLS) về mặt tiệm cận hiệu quả hơn so với mô hình Pooled OLS tổng hợp khi các thuộc tính hằng số thời gian có mặt.
2.1. Tính chất của mô hình FEM là gì?
Trước khi hồi quy mô hình ta cần lưu ý một số tính chất của mô hình FEM như sau:
- Thứ nhất, mô hình * được biết với tên gọi là mô hình các ảnh hưởng cố định một chiều (one-way fixed effects model), vì chúng ta cho phép các hệ số cắt khác nhau giữa các đơn vị chéo với nhau nhưng không khác nhau qua thời gian.
- Khi đưa thêm N biến giả về thời gian để đại diện cho T năm cùng với N biến giả cho các đơn vị chéo. Khi đó thì mô hình được gọi là mô hình các ảnh hưởng cố định hai chiều (two-way fixed effects model).
Tình chất đơn giản là 1 chiều và 2 chiều của mô hình FEM, sau đây xin mời các bạn qua phần hướng dẫn cách chạy mô hình FEM trong Stata.
2.2. Hồi quy mô hình tác động cố định FEM – Fixed Effects trong Stata
Đầu tiên tải về dữ liệu rồi cùng thực hành nhé:
Hình ảnh dữ liệu trong Excel:
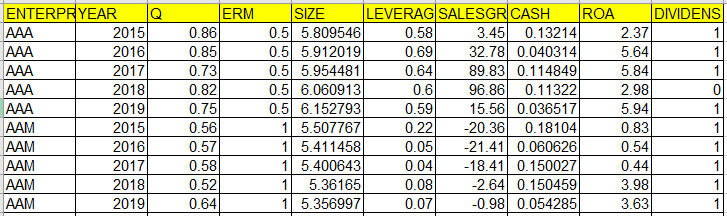Fem là gì? – Hồi quy mô hình FEM trong Stata
Bộ dữ liệu này gồm 30 quan sát gồm 6 công ty phi tài chính niêm yết trên sàn chứng khoán tại Việt Nam trong khoảng thời gian 5 năm từ 2015 đến 2019. Biến phụ thuộc là Q và các biến độc lập là ERM, SZE, LEVERAGE, SALESGROWTH, CASH, ROA và DIVIDENS.
Chú ý khi mới vào các bạn phải khai báo dữ liệu bảng cho Stata hiểu nhé! (Nếu chưa biết thì xem lại bài Cách khai báo Dữ liệu bảng của MOSL để hiểu nè).
Chạy hồi quy mô hình FEM Fixed Effects với cú pháp: xtreg [Biến phụ thuộc] + [Biến độc lập,..], fe như bên dưới:
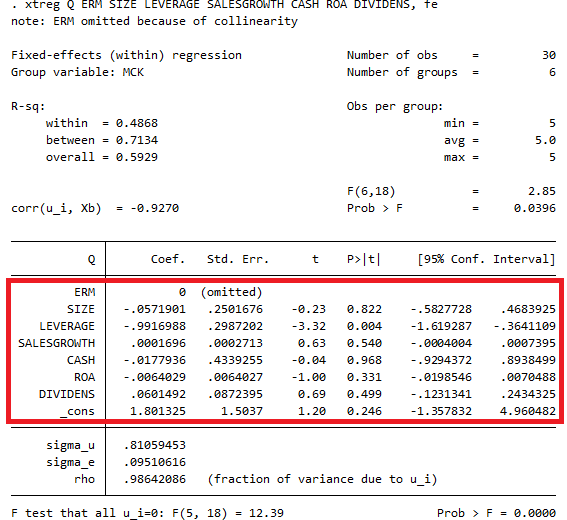FEM là gì? – Hồi quy mô hình FEM trong Stata
Kết quả hồi quy từ hình trên biến ERM bị omitted do hiện tượng thẳng hàng (collinearity) trong dữ liệu. Các biến còn lại trong mô hình được thể hiện trong bảng với hệ số tự do, độ lệch chuẩn, giá trị t, p-value và độ tin cậy.
Chú ý cực mạnh chỗ này nhé nếu bạn để ý phía ngay góc cuối bên phải có hệ số Prob > F = 0.0000 chính là giá trị p-value của kiểm định F test được chạy tự động hiển thị phía dưới cùng của bảng FEM ( 1 kiểm định giúp lựa chọn giữa OLS và FEM với giả thuyết H0: Mô hình phù hợp là OLS). Như vậy, mô hình phù hợp ở đây sẽ là mô hình FEM.
Funfact: Hồi quy tác động cố định FEM thực chất chính là hồi quy OLS + biến giả chủ thể ở đây là các mã công ty tạo nên (Cách này sẽ được trình bày dưới mục 6.2). Vì vậy bạn có thể sử dụng 1 trong 2 cách để thực hiện hồi quy FE cho nghiên cứu nhé! Ví dụ cụ thể như sau:
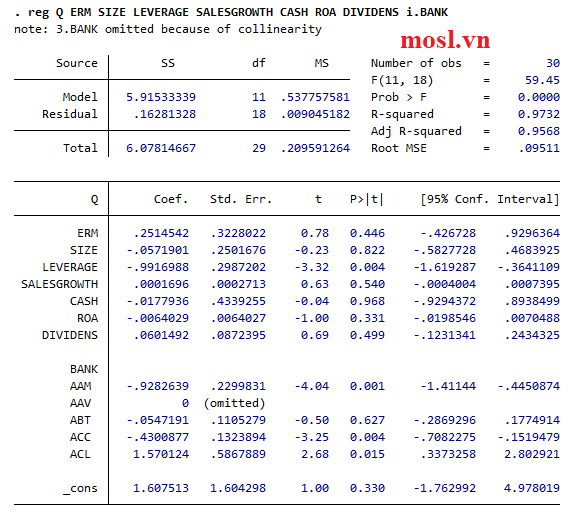FEM là gì? – Chuyển hoá Mô hình Pooled OLS thành FEM
Đơn giản tạo biến giả cho chủ thể của dữ liệu ở đây là các Công ty phi tài chính bằng câu lệnh i.BANK (BANK là tên đặt chung cho biến các cty phi tài chính) như hình thì bạn đã chuyển hoá thành công mô hình Pooled OLS thành mô hình FEM mà không cần phải chạy mô hình FEM rồi nhé!
2.3. Các kiểm định mô hình FEM
2.3.1. Kiểm định phương sai thay đổi trong Stata
Sử dụng lệnh: xttest3 (Lưu ý các bạn phải thực hiện lệnh này sau khi chạy hồi quy FEM nhé)
Giả thuyết:
H0: Mô hình xảy ra hiện tượng phương sai thay đổi
H1: Mô hình không xảy ra hiện tượng phương sai thay đổi
Kết quả:
FEM là gì? – Kiểm định phương sai thay đổi mô hình FEM
Từ kết quả kiểm định Wald trên ta thấy Prob>chi2 = 0.0884 > Mức ý nghĩa 5%, α = 0.05 nên chấp nhận H0 và kết luận mô hình xảy ra hiện tượng phương sai thay đổi.
Chú ý: Kiểm định Wald này cũng dùng để giúp đánh giá mô hình phù hợp trong hai mô hình OLS và FEM với giả thuyết H0: Mô hình phù hợp là OLS. Trong trường hợp trên ta bác bỏ H0 nên mô hình FEM sẽ là mô hình được chọn.
Xem thêm: Phương sai thay đổi là gì và cách khắc phục?
2.3.2. Kiểm định tự tương quan trong stata (Hay tương quan chuỗi)
Sử dụng lệnh: xtsserial [BPT] + [BĐL]
Giả thuyết:
H0: Mô hình không xảy ra hiện tượng tự tương quan
H1: Mô hình xảy ra hiện tượng tự tương quan
Kết quả:
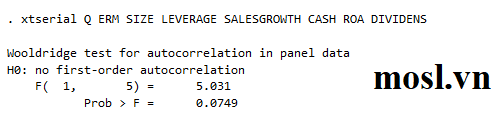FEM là gì? – Kiểm định tự tương quan mô hình FEM
Từ kết quả kiểm định Wooldridge trên ta thấy Prob>chi2 = 0.0749 > Mức ý nghĩa 5%, α = 0.05 nên chấp nhận H0 và kết luận mô hình không xảy ra hiện tượng tự tương quan.
Xem thêm: Tự tương quan là gì + cách khắc phục?
3. Mô hình tác động ngẫu nhiên REM (Random Effects Model)
Điểm khác biệt giữa mô hình ảnh hưởng ngẫu nhiên (REM) và mô hình ảnh hưởng cố định (FEM) được thể hiện ở sự biến động giữa các đơn vị.
- Nếu sự biến động giữa các đơn vị có tương quan đến biến độc lập – biến giải thích trong mô hình ảnh hưởng cố định thì trong mô hình ảnh hưởng ngẫu nhiên sự biến động giữa các đơn vị được giả sử là ngẫu nhiên và không tương quan đến các biến giải thích.
- Chính vì vậy, nếu sự khác biệt giữa các đơn vị có ảnh hưởng đến biến phụ thuộc thì REM sẽ thích hợp hơn so với FEM. Trong đó, phần dư của mỗi thực thể (không tương quan với biến giải thích) được xem là một biến giải thích mới.
Mô hình hồi quy mẫu tác động ngẫu nhiên REM là:
Yit = β1Xit + β2Xit + μit với i = 1, 2, …, N và t = 1, 2, …, T; μit = εi + uit
Trong đó:
εi : Sai số ngẫu nhiên có trung bình bằng 0 và phương sai là σ2
uit: Sai số thành phần kết hợp khác của cả đặc điểm riêng theo từng đối tượng và theo thời gian.
Một giả định quan trọng trong mô hình tác động ngẫu nhiên là thành phần sai số μit không tương quan với bất kì biến giải thích nào trong mô hình.
Các hiệu ứng ngẫu nhiên điều chỉnh cho mối tương quan nối tiếp được tạo ra bởi các thuộc tính hằng số thời gian không quan sát được.
Mô hình REM có các thuộc tính duy nhất, không đổi về thời gian của các cá nhân không tương quan với các giá trị hồi quy riêng lẻ. OLS tổng hợp có thể được sử dụng để lấy các ước tính không thiên vị và nhất quán của các tham số ngay cả khi có các thuộc tính hằng số thời gian, nhưng các tác động ngẫu nhiên sẽ hiệu quả hơn.
3.1. Hồi quy mô hình REM
Sử dụng bộ dữ liệu ở mục 2.3 trên thực hiện với cú pháp: xtreg [Biến phụ thuộc] + [Biến độc lập,..], re
Hồi quy mô hình REM trong Stata
Kết quả hồi quy mô hình REM trên cho các biến được thể hiện trong ô vuông đỏ khoanh tròn.
3.2. Các kiểm định mô hình REM
3.2.1. Kiểm định phương sai thay đổi
Sử dụng lệnh: xttest0 (Lưu ý các bạn phải thực hiện lệnh này sau khi chạy hồi quy REM nhé)
Kết quả:
Kiểm định phương sai thay đổi mô hình REM trong Stata
Tương tự mô hình FEM, thì kết quả kiểm tra phương sai mô hình REM bằng kiểm định Breusch and Pagan Lagrangian Multiplier trên ta thấy Prob>chibar2 = 1.0000 > Mức ý nghĩa 5%, α = 0.05 nên chấp nhận H0 và kết luận mô hình xảy ra hiện tượng phương sai thay đổi.
Kiểm định Breusch and Pagan LM này còn được thực hiện để làm kiểm định lựa chọn giữa OLS và REM với giả thuyết H0: Mô hình phù hợp là OLS. Trong trường hợp phía trên thì mô hình được chọn sẽ là mô hình OLS.
CỰC LƯU Ý: Kiểm định tự tương quan tương tự như đã thực hiện ở mô hình FEM phía trên. Ở đây tác giả mô phỏng cả 2 mô hình cho quý độc giả hiểu, khi vào nghiên cứu thì sẽ có 1 kiểm định lựa chọn giữa 2 mô hình này để tiến hành kiểm tra khuyết tật như trên là kiểm định Hausman Test. Qua phần tiếp để xem cách sử dụng kiểm định đó là gì nào.
4. Kiểm định lựa chọn mô hình
Thông qua lần hồi quy mô hình ban đầu bạn sẽ được mô hình OLS (hay còn gọi là Pooled OLS), và hai lần hồi quy mô hình tiếp sẽ cho bạn mô hình FEM và REM.
Tham khảo Mô hình OLS là gì và cách hồi quy? để biết nếu chưa rõ nè.
Vậy câu hỏi đặt ra ở đây là 1 trong 3 mô hình Pooled OLS, FE hay RE thì mô hình nào sẽ là phù hợp cho nghiên cứu?
Để giúp bạn hình dung tổng thể các phương pháp cần để lựa chọn các mô hình trên, MOSL xin chia sẽ hình bên dưới để hiểu rõ vấn đề nhé!
Fem là gì? – Bảng tổng hợp các kiểm định lựa chọn trong 3 mô hình Pooled OLS, FEM và REM
Hiện tại đa phần các nghiên cứu khi thực hiện đến đây đều chỉ chú trọng chọn 1 trong 2 mô hình FEM và REM (Các kiểm định lựa chọn giữa FEM + REM với OLS đã được thực hiện ở phía bên trên như Breusch Pagan LM; Wald Test, F Test) để tiếp tục nên MOSL xin hướng dẫn kiểm định Hausman Test (1978) theo Baltagi, 2008 và Gujarati, 2004 với cú pháp đơn giản như sau:
hausman [Tên đã đặt cho mô hình FEM] + [Tên đã đặt cho mô hình REM]
Chú ý: Để đặt tên cho mô hình thì sau khi hồi quy ví dụ MH FEM thì dùng lệnh: est sto + [tên tuỳ ý] (Ở đây MOSL đặt FEM và REM cho 2 mô hình để dễ hiểu nha)
Giả thuyết kiểm định Hausman:
H0: Mô hình REM
H1: Mô hình FEM
Fem là gì? – Kiểm định Hausman lựa chọn Fem và Rem
Từ kết quả ta thấy Prob>chi2 = 0.0038 < α = 0.05 nên Bác bỏ H0 và kết luận mô hình được chọn trong nghiên cứu chính là mô hình FEM.
Ở trên khi so sánh giữa REM & OLS bằng Breusch Pagan LM thì OLS phù hợp; FEM & OLS bằng F test và Wald test thì FEM là phù hợp; Vậy kết quả khi so sánh FEM và REM là chính xác và có thể suy luận ra được trước nha.
5. Mô hình GLS khắc phục khuyết tật từ mô hình được chọn
Ước lượng OLS cho mô hình tác động ngẫu nhiên sẽ cho các tham số ước lượng không chệch nhưng lại không hiệu quả. Sở dĩ như vậy là vì ước lượng OLS bỏ qua sự tự tương quan trong thành phần sai số μit. Để kết quả ước lượng không chệch và hiệu quả, chúng ta có thể sử dụng ước lượng GLS (Generalized Least Squares) để khắc phục hiện tượng sai số nhiễu tự tương quan và phương sai thay đổi trong mô hình được chọn thông qua kiểm định Hausman test phía trên, ở đây là mô hình REM.
- Bằng lệnh xtgls thì ước lượng GLS phù hợp với các mô hình tuyến tính bảng dữ liệu bằng cách sử dụng phương pháp FGLS ( Feasible Generalized Least Squares ) hay gọi là bình phương nhỏ nhất tổng quát khả thi. Lệnh này cho phép ước tính với sự hiện diện của tự tương quan AR (1) trong bảng và tương quan mặt cắt và phương sai thay đổi giữa các bảng.
Sử dụng dữ liệu như cũ và cú pháp như sau: xtgls [BPT][BĐL],panels(heteroskedastic) corr(ar1)
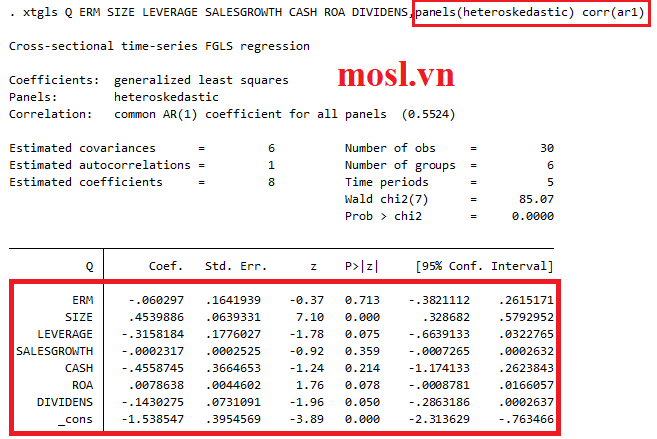Mô hình GLS là gì?
Sau dấy phẩy thì lệnh panels(heteroskedastic) dùng để khắc phục phương sai thay đổi nếu MH được chọn bị khuyết tật và lệnh corr(ar1) để khắc phục tự tương quan.
LƯU Ý CỰC MẠNH: Ở phần 4 thì mô hình REM được chọn chỉ bị khuyết tật phương sai thay đổi nên nếu chạy FGLS thì các bạn chỉ cần chạy với lệnh panels(heteroskedastic) thôi nhé, do MOSL muốn chạy full code cho các bạn dễ hình dung nè!
LƯU Ý MẠNH TIẾP THEO: Cách đọc kết quả Stata từ bảng kết quả hồi quy của 3 mô hình FEM; REM; GLS đều giống như cách đọc trong mô hình OLS. Xem cách đọc mô hình hồi quy tại đây
Vậy là đến đây bạn có thể kết luận mô hình cuối cùng cho nghiên cứu, mô hình được xem là cao cấp nhất loại bỏ các khuyết tật rồi nhé!
6. Mở rộng thêm thông tin về các mô hình hồi quy
6.1. Mô hình bảng động (Dynamic Panel Model)
Xem thêm: Mô hình hiệu ứng động không quan sát
Ngược lại với mô hình dữ liệu bảng điều khiển tiêu chuẩn, mô hình bảng điều khiển động cũng bao gồm các giá trị trễ của biến phụ thuộc dưới dạng các biến hồi quy. Ví dụ: bao gồm một độ trễ của biến phụ thuộc sẽ tạo ra:
Các giả định của mô hình hiệu ứng cố định và hiệu ứng ngẫu nhiên bị vi phạm trong cài đặt này. Thay vào đó, các học viên sử dụng một kỹ thuật như công cụ ước lượng Arellano-Bond.
6.2. Ước lượng LSDV (Least Squares Dummy Variable Estimator) của OLS
Ước lượng LSDV (Least Squares Dummy Variable Estimator) là ước lượng biến giả bình phương tối thiểu là một dạng của ước lượng OLS.
Quá trình thực hiện ước lượng lSDV theo 2 bước như sau:
- Bước 1: Tạo một biến giả tương ứng với một đối tượng trong mẫu.
- Bước 2: Hồi quy OLS biến phụ thuộc Y theo N-1 biến giả và các biến giải thích.
Ở dữ liệu này ta có 6 công ty, thì ta sẽ tạo ra 6 biến giả, và sẽ đưa 4-1 biến giả này vào hồi quy OLS đơn giản với lệnh i.công ty (STATA tiện quá nhỉ!) thêm vào code khi hồi quy mô hình OLS ban đầu.
6.3. Các cách khác để lựa chọn giữa FEM và REM
Rõ ràng, một trong những thách thức của chúng ta khi phân tích dữ liệu mảng là lựa chọn REM hay FEM là gì khi phân tích? Về vấn đề này, Judge et al. (2007) chỉ ra một số dấu hiệu như cho việc lựa chọn mô hình như sau:
- Nếu T là lớn và N là nhỏ thì rất có thể không tồn tại khác biệt lớn giữa các ước lượng thu được từ REM và FEM. Sự lựa chọn mô hình lúc này chỉ đơn thuần là căn cứ vào sự thuận tiện khi tính toán. Theo tiêu chí này thì FEM thường được ưu tiêu hơn.
- Khi T là nhỏ và N là lớn thì các ước lượng thu được từ hai phương pháp có thể khác biệt đáng kể. Nhắc lại rằng trong mô hình REM, βi =γ1 + εi với đại diện cho bộ phận sai số ngẫu nhiên ứng với cá thể thứ i trong mẫu nghiên cứu. Trong khi đó, ở mô hình FEM thì ta coi βi là bộ phận cố định chứ không phải là biến ngẫu nhiên. Cách tiếp cận FEM là phù hợp nếu chúng ta tin tưởng mạnh mẽ rằng các cá thể trong mẫu nghiên cứu không được lựa chọn ngẫu nhiên từ một tổng thể lớn hơn. Ngược lại, nếu các cá thể trong mẫu được lựa chọn ngẫu nhiên thì REM là phù hợp hơn. Vì trong tình huống này các thống kê suy luận là không có điều kiện (unconditional).
- Nếu bộ phận sai số ngẫu nhiên εi và một hay một số biến độc lập là tương quan thì các ước lượng thu được từ FEM là các ước lượng chệch (biased) trong khi đó các ước lượng thu được từ FEM là các ước lượng không chệch (unbiased).
- Nếu T nhỏ và N là lớn và các giả định nền tảng cho REM là đúng thì các ước lượng thu được từ REM là hiệu quả hơn so với các ước lượng thu được từ FEM (Taylor, 1980).
Tuy GLS là mô hình cao cấp nhất sau khi khắc phục các khuyết tật như phương sai thay đổi và tự tương quan nhưng nó vẫn chưa thể khắc phục được hiện tượng nội sinh và phải bằng kiểm định GMM thì ta mới khắc phục được vấn đề này. Nên nhớ đón xem toàn bộ vấn đề xoay quanh mô hình GMM của MOSL tại đây nhé!
7. Tổng kết
Tổng hợp lại kiến thức MOSL đã cung cấp đến độc giả đơn giản như sau:
1. Khái niệm mô hình REM và FEM là gì?
2. Hồi quy mô hình FEM và REM trong Stata
3. Tiến hành lựa chọn 3 mô hình FEM, REM, POOLED OLS bằng kiểm định Hausman Test, Breusch – Pagan LM, Chow Test …
4. Kiểm tra khuyết tật mô hình được chọn và chạy mô hình GLS để khắc phục
5. Kết luận mô hình cuối cùng cho nghiên cứu
Đến đây, MOSL xin chúc các bạn học tập và làm việc hiệu quả!
Xem thêm: Xử lý số liệu và hỗ trợ chạy Stata của Mosl.vn
Tag: Fem là gì? Fem là j? Mô hình Fem là gì? Mô hình Tác động cố định FEM là gì? Hồi mô hình FEM là gì trong Stata? Mô hình OLS trong kinh tế lượng.