Giới thiệu
Support Vector Machine (SVM) là một mô hình phân loại hoạt động bằng việc xây dựng một siêu phẳng (hyperplane) có (n – 1) chiều trong không gian n chiều của dữ liệu sao cho siêu phẳng này phân loại các lớp một cách tối ưu nhất. Nói cách khác, cho một tập dữ liệu có nhãn (học có giám sát), thuật toán sẽ dựa trên dữ liệu học để xây dựng một siêu phẳng tối ưu được sử dụng để phân loại dữ liệu mới. Ở không gian 2 chiều thì siêu phẳng này là 1 đường thẳng phân cách chia mặt phẳng không gian thành 2 phần tương ứng 2 lớp với mỗi lớp nằm ở 1 phía của đường thẳng.
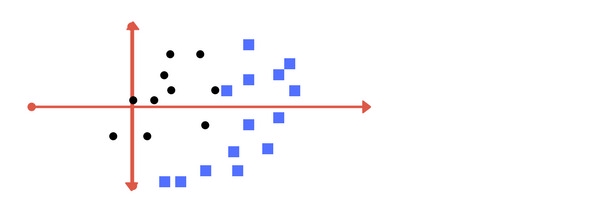
Ví dụ, ta có các điểm dữ liệu như hình dưới đây với mỗi điểm thuộc 1 trong 2 lớp cho trước:
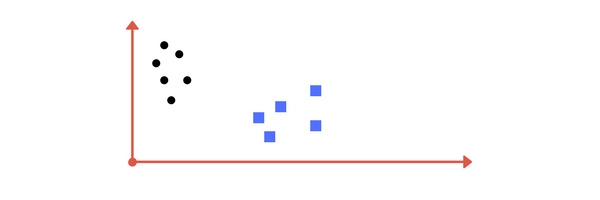
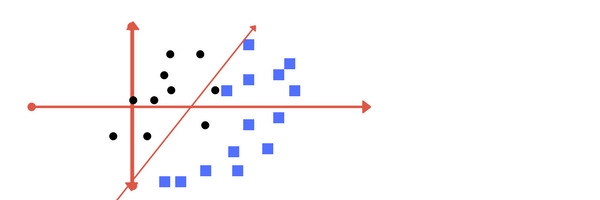
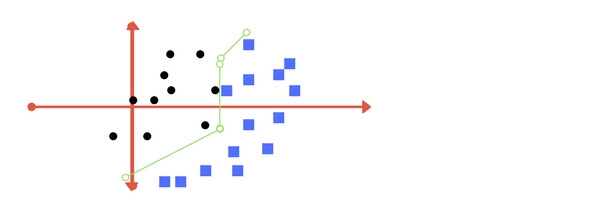
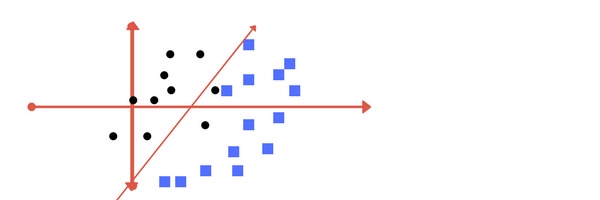
Một đường thẳng phân cách có thể được vẽ như sau:
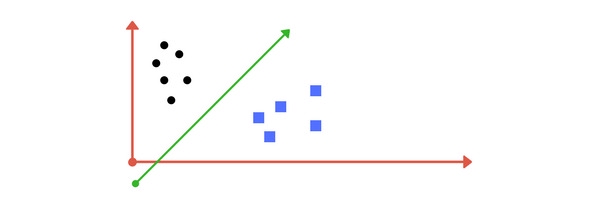
Đường thẳng này chia cách khá tốt 2 lớp trên mặt phẳng. Tất cả những điểm dữ liệu nằm bên trái đường thẳng đều thuộc về lớp hình tròn và những điểm nằm ở bên phải thuộc về lớp hình vuông. Nhiệm vụ của SVM chính là tìm ra đường thẳng / siêu phẳng phân cách cách sao cho phân loại dữ liệu tốt nhất có thể.
Tổng quát về SVM
Ví dụ trên có các điểm dữ liệu thuộc 2 lớp có thể phân cách trực tiếp bằng 1 đường thẳng. Tuy nhiên, không phải dạng dữ liệu nào cũng đơn giản được như vậy. Ví dụ với dạng dữ liệu như hình dưới:
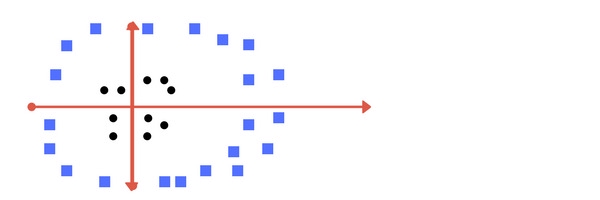
Với các điểm dữ liệu thế này thì không thể phân cách chỉ bằng 1 đường thẳng. Các điểm dữ liệu của lớp hình tròn nằm tập trung ở xung quanh gốc tọa độ và để phân cách chúng với các điểm dữ liệu của lớp hình vuông thì phải sử dụng đường cong. Trong trường hợp này, đường cong đơn giản nhất chúng ta có thể nghĩ đến là hình tròn. Ta áp dụng điều này bằng cách thêm 1 chiều không gian z = x2 + y2. Nếu các bạn để ý thì sẽ thấy z chính là công thức của 1 hình tròn có tâm tại gốc tọa độ. Ta sẽ thử vẽ lại đồ thị của các điểm dữ liệu trên không gian zy:
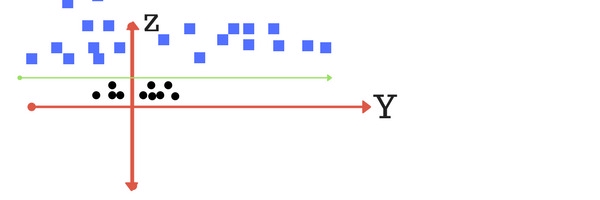
Tại không gian này, các điểm dữ liệu đã có thể phân cách bằng 1 đường thẳng. Nói cách khác, với chiều không gian mới z, việc phân loại đã trở nên đơn giản hơn rất nhiều. Quay lại với không gian xy, các điểm dữ liệu sẽ được phân cách bằng một hình tròn:

Việc sử dụng thủ thuật biến đổi đại số và thêm chiều không gian z được gọi là phương pháp kernels. Với các tập dữ liệu khác nhau, bạn có thể sử dụng các kernels có sẵn hoặc sẽ phải sáng tạo ra 1 kernel mới để phù hợp với bài toán của mình.
Tuy nhiên, công việc chưa dừng lại ở đó. Giả sử rằng dữ liệu của bạn không ổn định và các điểm dữ liệu không phân cách nhau một cách rõ ràng, thâm chí còn chông chéo lên nhau. Xét ví dụ dưới đây:
Với dữ liệu như thế này, việc phân cách các lớp chỉ bằng một đường thẳng là không khả thị. Cùng xét 2 cách phân chia dưới đây:
Vẫn sử dụng 1 đường thẳng phân cách nhưng không thể phân loại đúng được tất cả các điểm dữ liệu
Các điểm dữ liệu đã được phân loại đúng nhưng phải sử dụng tới 3 đường thẳng phân cách.
Vậy cách nào là đúng ? Câu trả lời là cả 2 cách đều chấp nhận được. Cách 1 sẽ bỏ qua các điểm dữ liệu bất thường (outliner) để đổi lấy tốc độ tính toán. Cách 2 sẽ không bỏ qua điểm dữ liệu nào và đạt độ phân cách hoàn hảo nhưng bù lại sẽ độ phức tạp hơn và tốc độ tính toán sẽ chậm hơn cách 1. Việc bạn ưu tiên chọn cách nào được thể hiện qua việc điều chỉnh các tham số của mô hình SVM và đó là nội dung phần tiếp theo.
Điều chinh các tham số: Kernel, Regularization, Gamma và Margin
- Kernel
Quá trình xây dựng siêu phẳng phân cách trong SVM được thực hiện qua các phép biển đổi đại số. Với kernel dạng tuyến tính (linear kernel) công thức dùng để dự đoán những điểm dữ liệu mới là: thực hiện tích vô hướng giữa đầu vào (x) với mỗi support vector (xi) như sau: f(x) = B(0) + sum(ai (x, xi)). Các hệ số B0 và ai (cho mỗi đầu vào) phải được ước tính từ dữ liệu học. Với kernel dạng đa thức (polynomial kernel) có thể được viết dưới dạng: K(x, xi) = 1 + sum(x, xi) ^ d. Còn với kernel dạng lũy thừa (exponential kernel) có dạng: K(x, xi) = exp(-gamma * sum((x – xi2)).
Kernel dạng đa thức và dạng lũy thừa tính toán đường phân cách ở những chiều không gian cao hơn và được gọi là kernel trick.
- Regularization
Tham số Regularization ( được nhắc đến trong thư viên sklearn là tham số C) điều chỉnh việc có nên bỏ qua các điểm dữ liệu bất thường trong quá trình tối ưu mô hình SVM. Nếu tham số này có giá trị lớn, quá trình tối ưu sẽ chọn một siêu phẳng sao cho siêu phẳng này phân cách tất cả các điểm dữ liệu một cách tốt nhất, từ đó khoảng cách giữa siêu phẳng tới các điểm dữ liệu của 2 lớp sẽ có giá trị nhỏ (small-margin). Ngược lại, khi tham số này có giá trị nhỏ, siêu phẳng sẽ được xây dựng sao cho khoảng cách với các điểm dữ liệu của 2 lớp có giá trị lớn (large-margin), kể cả khi siêu phẳng này sẽ phân loại sai nhiều điểm dữ liệu hơn.
Dưới đây là các ví dụ về 2 trường hợp chọn tham số C:
Tham số C có giá trị nhỏ
Tham số C có giá trị lớn
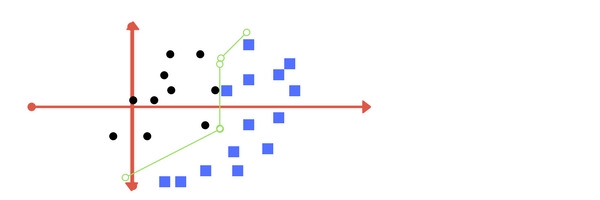
- Gamma
Tham số gamma xác định việc sử dụng bao nhiêu điểm dữ liệu cho việc xây dựng siêu phẳng phân cách. Với giá trị gamma nhỏ, các điểm dữ liệu nằm xa đường phân cách sẽ được sử dụng trong việc tính toán đường phân cách. Ngược lại, với giá trị gamma lớn, chỉ những điểm nằm gần đường phân cách mới được sử dụng để tính toán.
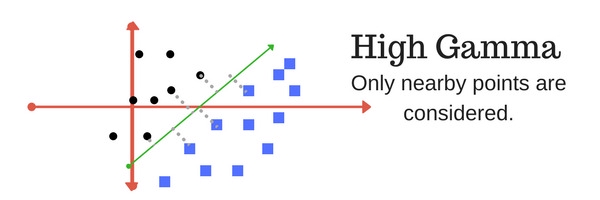
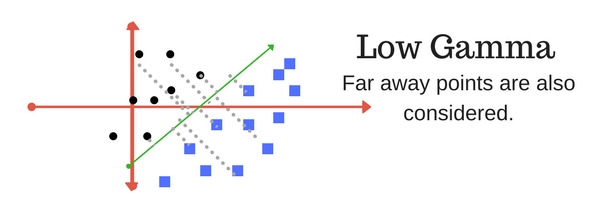
- Margin
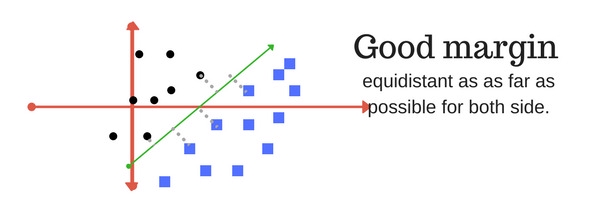
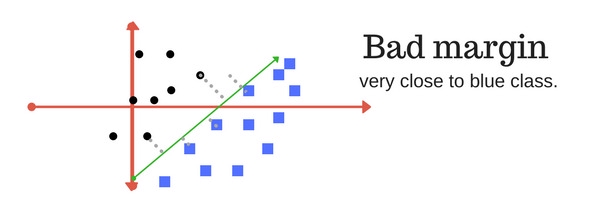
Margin trong SVM là khoảng cách giữa siêu phẳng phân cách với các điểm dữ liệu gần nó nhất. Khoảng cách này đối với các điểm dữ liệu gần nhất của cả 2 lớp càng lớn thì mô hình càng phân loại chính xác. Các ví dụ về margin:
SVM có margin tốt : khoảng cách lớn và cân bằng giữa siêu phẳng và các điểm dữ liệu của 2 lớp
SVM có margin tồi: khoảng cách không cân bằng & nghiêng hẳn về 1 phía
Vậy là qua bài viết này, chúng ta đã tìm hiểu về Support Vector Machine, một phương pháp được sử dụng phổ biến trong Machine Learning. Các bạn có thể tham khảo paper gốc về SVM để tìm hiểu kỹ hơn: https://link.springer.com/article/10.1007/BF00994018.
Cảm ơn các bạn đã đọc bài viết :D.
Nguồn: Medium Support Vector Machine Theory
